CIRCLE GEOMWTERY FOR BEGINNERS
Explore the amazing field of circle Geometry For Beginners! You will learn the key ideas, equations, and problem-solving techniques from this succinct manual.

Circle geometry is an interesting branch of mathematics that examines the properties and characteristics of circles. This includes arcs, sectors, tangents, etc. Not only is it important for making pizzas, but also for navigating using GPS and solving real world problems.
This guide will take you through the worlds of circle geometry. We will start by introducing the basic terms and concepts before moving on to important theorems. You’ll be able to understand circles and how they are used in our everyday lives by the end. Let’s get started!
A GENTLE INTRODUCTION TO CIRCLE TERMS AND CONCEPTS
The secret to unlocking the mysteries of circles is to comprehend the foundations of circle geometry.
Points that are evenly spaced from a center point make up a circle. As a result, a flawless round form is produced. The radius of a circular form is the separation between its center and any other point on the shape. The straight line that goes through the center when the radius is multiplied by two is called the “diameter.”
Now let’s discuss “circumference,” which is the length of time it takes to go around a circle. For this, multiply the magic number “pi” (approximately 3.14), by the circle’s diameter (C = Pd) or the doubled radius (2pr).
The arc is another fascinating feature of a circle.It is a section that connects two spots on the circular surface’s edge.These basic concepts lay the groundwork for exploring more complex aspects of circle geometries such as sectors, tangents and the relationship between angles and circles.Gaining an understanding of these ideas can lead to innovative approaches to problem-solving and practical applications. Let’s go exploring some more!
UNPACKING KEY THEOREMS AND FORMULAS
Find out how to solve circle geometry problems using key tools. These theorems offer shortcuts for navigating the world of circles. They include the circular adaptation of the Pythagorean Theorem, insights into central angles, and chord-chord powers. Learn them to solve problems with confidence!

Decoding the secrets behind circle geometry is similar to decoding a culinary masterpiece. Consider, for example, the “Inscribed Angle Theorem,” which reveals that an angle formed from two lines extending from the edge of a pizza is half as large as the angle on the whole pizza. The ‘Central Angle Theorem’ is a complementary theory that equates the angle in the circle’s middle to the angular extent of the pizza slice. We gain a better understanding of the circular space when we use formulas such as area (A = Pr2) and circumference (2pr). This journey through circle geometry enriches the problem-solving process and opens up a variety of applications from architecture to arts.
LET’s GET TO KNOW ARCS, SECTORS, AND TANGENTS
A ‘arc’ can be compared to the edge of a circular slice, similar to the crust of a tasty slice of pizza.
Imagine’sectors’ as actual pizza slices delineated by the two radii, and the arc that they intersect within the circle.
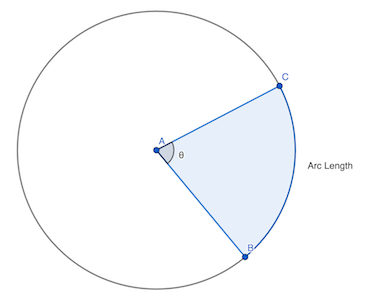
Think of a “tangent” as a line that, at one point, just barely touches the circle.It’s like skimming over the crust, but without actually breaking it.
You’ll find that these ideas make problem-solving easier, especially when it comes to solving mathematical puzzles with circles.
CONCLUSION
Explore the fascinating world of circle geometry. Every curve has a tale to tell. Explore the complex dance of shapes in our world, from the elegant arcs to tantalizing tangents. Discover the mathematical magic hidden in these round wonders. Join the adventure where circles are more than just shapes, they’re gateways to an infinite universe.
