WHAT ACTUALLY IS SINE, COSINE, AND TANGENT?
The study of trigonometry is quite interesting! Discover what Actually Is Sine Cosine and Tangent? the fundamental elements of solving right triangles: sine, cosine and tangent. Immerse yourself in this fascinating world where math meets the real-world. These essential functions will help you tackle geometry with confidence. Start your trigonometric adventure today!
Discover the fascinating world of trigonometry where angles and triangles reveal a mathematical realm of wonders! Imagine yourself on top of a mountain with panoramic views or admiring an airplane flying across the sky. Trigonometry’s magical trio: sine, cosine and tangent, can decode these everyday wonders. Join us for an exciting journey through architecture, space and beyond. Each calculation will reveal the secrets of our universe. Explore the magnificence of trigonometry right now!
THE FABULOUS TRIO OF TRIGONOMETRY: SINE, COSINE AND TANGENT
Imagine a triangle in the form of a family tableau. The hypotenuse is the nurturing parent who cradles its children, the sides, with tender care.
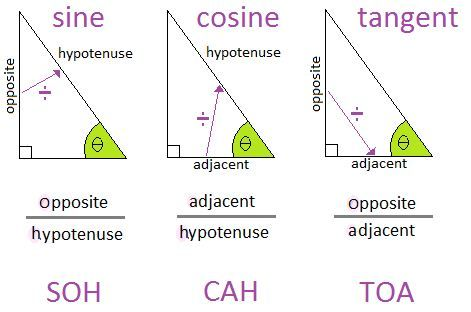
Sine (sin), the rebellious rebel, is represented by the ratio of the length of one side (the rebellious kid) to the loving span of the hypotenuse (the parent).
Cosine (cos), on the other hand, represents the obedient sibling. It is the ratio between the adjacent side of the hypotenuse (the obedient kid) and the hypotenuse.
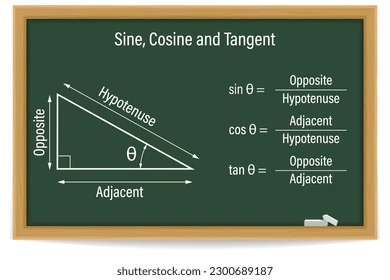
The dynamic link between the two siblings is Tangent (tan), which represents the relationship between cos and sin, similar to the bond that exists between family members.
The ancient Babylonians and Greeks used triangles’ mystical properties to solve celestial mysteries, chart uncharted seas and build architectural wonders.
Over the centuries, these primitive concepts have evolved to modern trigonometry. It offers a lens that transforms how we see angles and triangles.
In essence:
- Sin (sin): Imagine your triangle as an enormous mountain.The ratio of its height (opposite) to the distance (hypotenuse) from the summit to the base camp is represented by the sin.
- Cosine (cos), also known as the ratio of distance in a right angled triangle, is the same as measuring the distance from the foot (the hypotenuse) to the base (the base).
- Tangent (tan), a luminary ratio that represents the height of the mountain in relation to its base, as well as the sine to cosine correlation.
These trigonometric functions are not only dazzling with their triangle wizardry but also weave into a variety of disciplines, such as physics and engineering, computer graphics and signal processing. They have become indispensable tools in our arsenal.
TRIGNOMETRY: THE VERSATILE MATHEMATICIAN’s BEST FRIEND
There is nothing like trigonometry’s adaptability. Sine, cosine and tangent have been the secret force behind many innovations, from skyscrapers, computer graphics, to economics.
Trigonometric functions such as sine and cosine, are essential tools in the world of architecture. They provide precision and creativity. These functions are used by architects to calculate the slope of staircases and design complex roof trusses
Trigonometry is used to create immersive virtual environments in the world of 3D modelling.
Trigonometry has a wide range of applications. These mathematical tools are used by physicists to study phenomena like projectile motion, forces on inclined planes and more. Computer scientists use them to create captivating virtual reality environments.
The ancient building of pyramids and the modern landing of Mars rovers have all left a lasting impression on our understanding of how the universe works.
THE ENDURING LEGACY OF TRIGONOMETRY
Trigonometry is a legacy that has been left by the Babylonians, Greeks, and Indians. They recognized its importance in solving problems in astronomy and navigation as well as construction.
Hipparchus and other Greek mathematicians laid the foundation, but scholars such as Ptolemy developed it further, introducing trigonometry spherical.

In the past, Islamic mathematicians and Renaissance thinkers have added to its complexity. Trigonometry is still shaping our world today, from space exploration to architecture, and computer graphics. Thanks to sine, cosine, tangent, the three enduring heroes of trigonometry.
CONCLUSION
As a conclusion, sine cosine and tangent are like the keys of a grand piano that each contribute to the harmony of trigonometry. These tools are not only invaluable in shaping our understanding of the Universe, but they also make complex problems more approachable and reveal hidden patterns.
Their versatility is unmatched, with applications in architecture, physics and computer graphics. The sine, cosine, and tangent narrative highlights the creative and inquisitive nature of people. It shows how mathematical melodies have continued to resonate throughout time and continue to influence future discoveries and innovations.
Let’s honor these unsung heroes on our exciting journey through the fascinating world of trigonometry where each calculation is a source of revelation and enlightenment.
