WHAT ARE THE TYPES OF ANGLES IN GEOMETRY?
Dive into the wonderful realm of What are the Types of Angles in Geometry? and discover the interesting world of angles! Discover the mysteries of acute, obtuse and right angles – click to learn more and become an expert in the world of angles.
Discover the secrets of geometric shapes and patterns!
Geometry orchestrates our world in a silent way. From the towering skyscrapers of the city to the triumphant trajectory a soccer ball takes, it is geometry that creates the beauty we see around us. Today, angles—one of its unsung heroes—will be highlighted. Angles are those fascinating spaces between intersecting planes or lines that play a vital role in the intricate tapestry geometry. Angles are everywhere. From engineering feats and breathtaking architecture to the natural world and our favorite pieces of art.
We will discuss the distinctive qualities of acute, right, and obtuse angles, among others. Just as different dog breeds boast distinct traits, so do angles. You can gain access to the mathematical world’s most exciting corners by mastering the recognition and understanding of angles.
Are you ready for this journey? We will explore the world of angles to unlock the secrets of geometrical geometry.
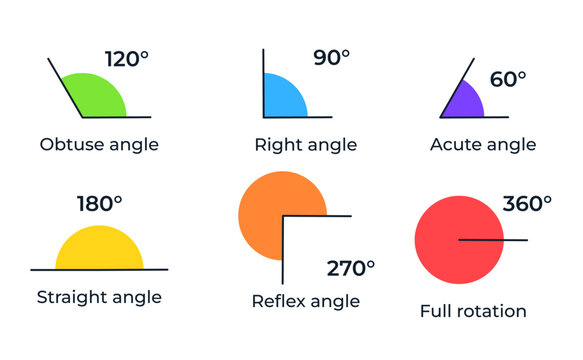
ANGLE FUNDAMENTALS: RIGHT, ACUTE, OBTUSE, AND MORE!
Angles are like the kisses of a romance in this story. They’re formed when two lines or rays intersect at one vertex. Their space is measured in degrees, revealing their essence.
The right angle is a 90-degree luminary that lends structure to shapes such as rectangles and squares. The Pythagorean Theorem illuminates the path for solving triangle mysteries.
Our cast of angles still has a lot to offer. The triangle family is enriched by the addition of obtuse and acute angles.
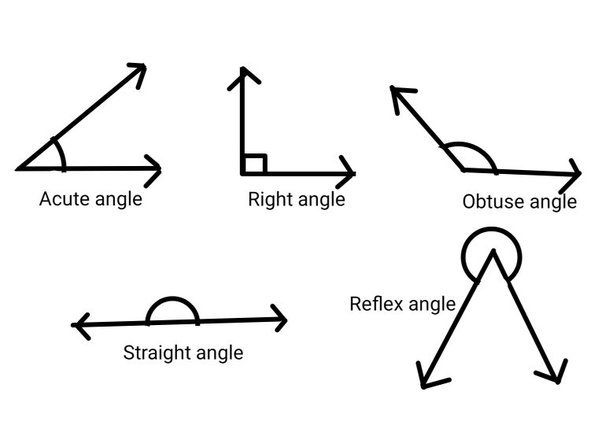
There’s also the straight angle, which is a 180-degree half-turn that looks like a line running from the vertex. It reminds me of a limbo-pole.
The enigmatic reflexive angles, which extend beyond 180 degrees but below 360, are not common in everyday geometry problems, but they play a crucial role in advanced studies such as solid geometry and spherical triangles, like a rare but essential dark horse.
Discovering these angles is like discovering a secret chamber full of intrigue.
Unlock the secrets of geometry to unlock the doors to endless mathematical treasures.
DIVING DEEPER: ADVANCED ANGLE ADVENTURES
Do you know what angle bisectors are?
The remarkable line segments or rays have the ability to divide any angle into two equal halves. This splitting creates the incenter point. It is important across diverse fields from robotics to navigation systems.
Transversal angles are created when a line, the transversal, intersects with two or more parallels lines. This creates a “angle party” that is both fascinating and exciting.
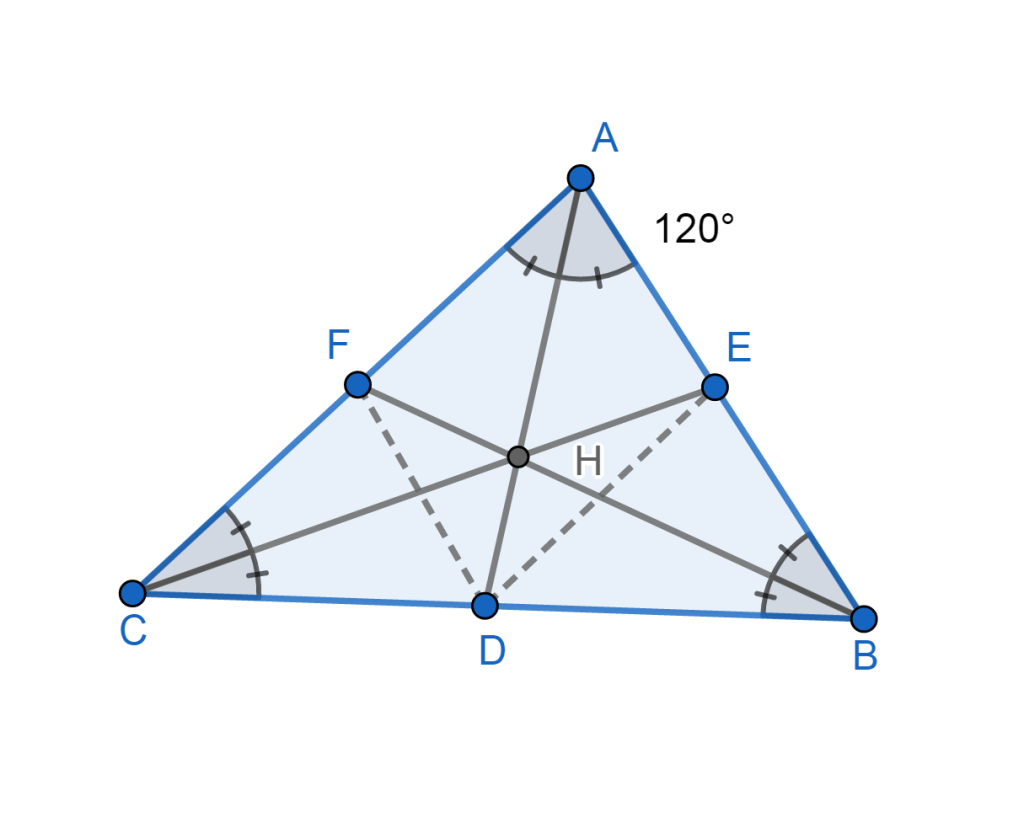
This dynamic grouping includes comparable angles and different internal angles among its many characters. We also encounter alternate exterior angles and consecutive interior angle, all with their own unique properties and relationships, similar to siblings.
These angles can be congruent by sharing the same measures or supplementary by adding up to 180°. These intricate connections allow us to solve complex geometric puzzles, similar to solving Rubik’s Cube, and to navigate challenges from triangles to circles and polygons with confidence.
COMPLEMENTARY AND SUPPLEMENTARY ANGLES: THE HARMONIOUS DUO
Geometry is more than just a technical subject. It embodies balance and harmony, as shown by the complementary and supplementary angles.
Complementary angles are like two friends who can’t be separated. They complete each other and sum up to 90 degrees. In contrast, supplementary angles are two halves that make up a complete 180 degrees.
Solving a variety of geometric problems requires an understanding of these angle connections. Civil engineers and architects use these principles to design efficient road networks. Artists also employ these ideas to produce visually arresting pieces. These principles are relevant in sports as well. Angle relationships are a natural tool used by basketball players to calculate shots and increase their scoring opportunities. Geometric concepts improve our critical thinking, as well as our athletic ability and problem-solving abilities.
CONCLUSION
The fascinating world of angles in Geometry is now over!
You’ve already laid the foundation to explore more complex angles such as linear pairs and vertical angles.
Each geometric element reveals the elegance and beauty inherent in geometry. From the harmonious interplay between complementary and supplementary angle to the fascinating dynamics of the angles formed by transversals.
Next time you see the corners of a book, or the angles on a soccer goal take a minute to admire the unsung heroes in geometry: angles!
Explore, expand your knowledge and, above all, enjoy the thrill of discovering the wonders that are geometry!
