TANGENTS & SECANTS: THE BEST FRIENDS OF CIRCLE GEOMETRY
Discover the secrets of Tangents & Secants: The Best Friends of Circle Geometry, curves, shapes and tangents by exploring secants and tangents. Explore their differences to uncover captivating geometric relationships.

Welcome to the world where secants and tangents rule supreme!
This guide will introduce you to the circle geometry stars, with clear explanations and examples that highlight their role.
Imagine tangents as loyal companions who weave their way through curves and shapes. Together, they are the foundation of geometric exploration. They shed light on mathematical concepts as well as real-world applications.
Discover the secrets of secants and tangents by embarking on an interesting adventure with us. We will provide you with insights that will improve your understanding of geometrical concepts and their relevance in everyday life.
A ROUND OF BASIC CIRCLE CONCEPTS
We’ll review some of the basic concepts about circles in order to understand tangents, secants and tangents.
Imagine a circular dartboard with the center representing the bullseye, and the radius being the distance between the center and any point. The line that touches two locations at the edge and goes through the center is known as the circumference of a circle.
Imagine throwing two darts onto the board. You can create a central angle by connecting the bullseye to the two points where the darts landed. You can form a chord if the darts are landed on the edges and the points are connected. By connecting the points in the bullseye, you can create an engraved angle.
We’ll go over tangents, secants and circle basics in the next section. Let’s get started!
GETTING FRIENDLY WITH TANGENTS
Imagine a little insect gliding across a basketball’s surface. It makes one contact with the ball before moving on without crossing it. Simply put, a tangent is a straight line that touches the circle only once.
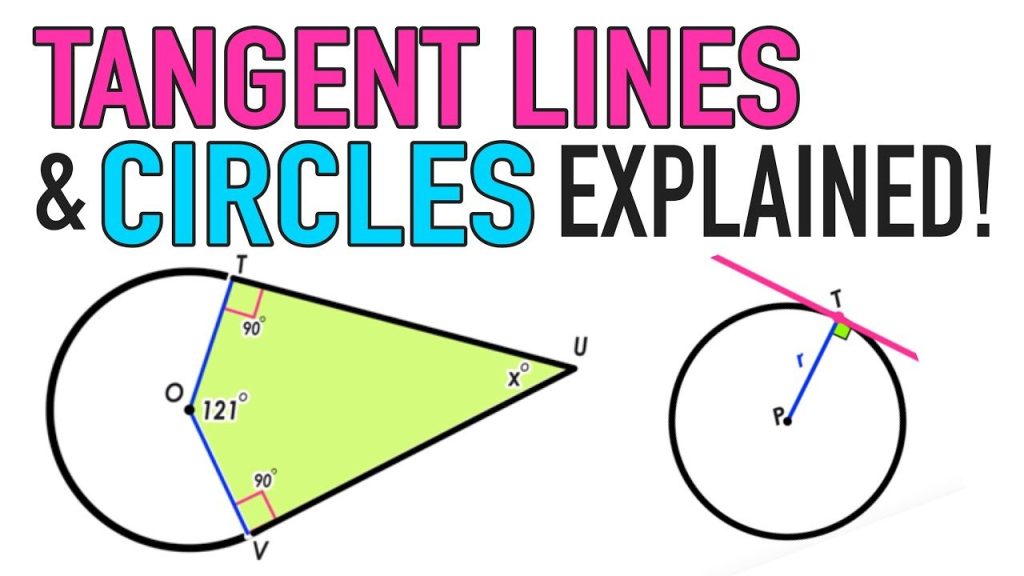
At the point of contact, tangents and the ball’s radius produce a right angle. The ant will form a perfect “L” shape if you halt it at the place where it meets the ball and draw a straight line from this point to the ball’s center.If two ants begin at the same place and travel along two different tangents, they will both walk the same distance in order to reach the circle.This is called the Two-Tangent Theorem.
Tangents are quite helpful. They are used by engineers to create safe, curved racetracks and roadways. They are used by physicists to investigate object motion and by architects for the building of domes.
DIVING INTO THE WORLD OF SECANTS
Visualize a delicateruby-throated hummingbird gracefully traversing through a circular window opening, entering at one point on the circumference and exiting at another.This elegant flight path is the essence of the’secant,’ which is a line that crosses the circle in two different points.
Secants and tangents are both valuable, but they differ in their uniqueness. Secants have many uses in mathematics. In trigonometry for example, the secant’ is the reciprocal function of the cosine’, which is pivotal in triangle calculations. In calculus, secants are used to comprehend rates of change and approximate values.Secants are more than just mathematical abstractions. They have a real-world application. Secants are used to design structures like bridges, arches, and domes. They also provide insights into celestial physics, which helps us understand planetary orbits.
CONCLUSION
The tangents, and secants, are the unsung heroes in geometry. They weave their magic both in abstract mathematical realms, and real-world practical applications. Their influence is profound and far-reaching. Keep exploring the mathematics of the universe and unraveling its mysteries!
