EVERYTHING YOU NEED TO KNOW ABOUT REFLEXIVE PROPERTY
Uncover the everything you need to know about the reflexive property. The fundamental idea of mathematics is that all quantities are equal to one another. This concise overview explains its importance and relevance to real-life.

IS MATH A MYSTERY? THE REFLEXIVE PROPERTY
Math can be intimidating for many students due to its complex terminology and concepts. Let’s solve the mystery of the “reflexive property”, a mathematical superpower that is hidden in numbers and shapes. This concept simplifies algebra, geometry and logic. Math becomes easier for everyone.
SO, wHAT’s tHE REFLEXIVE PROPERTY?
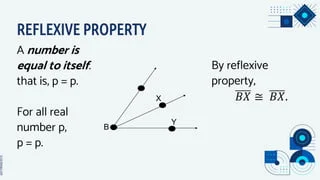
At first, the Reflexive Property might seem like a simple concept: everything in mathematics is equal to itself. Despite its apparent simplicity, this idea is a useful tool for resolving challenging mathematical issues. Understanding the Reflexive Property’s versatility and importance not only improves problem-solving abilities, but also builds confidence when tackling difficult math problems. Explore its real-world applications to understand its true value.

aNCIENT GREEK MATHEMATICIANS
Imagine the reflexive property is the superhero of mathematics.It possesses the ability to guarantee that everything is equal. This principle may appear simple, but it is the foundation for many operations and proofs in various mathematical disciplines.
The reflexive property is akin in essence to the statement “I am myself, and my twin will always be my twin” when it comes to math. The ancient Greek mathematicians, such as Euclid, recognized this concept during the development geometric theories. Numerous areas of mathematics, such as algebra, geometry, and logic, have adopted it. Consider a box of candies with different shapes to illustrate the significance. We assert, through the lens of the “reflexive property”, that “every candy has the same shape as itself,” which facilitates the grouping of similar candies in coherent groups – a fundamental principle of set theory.
In the world of algebra, this property is a trusted sidekick. It ensures that both sides of a equation are equal, which preserves logic and facilitates accurate equation solving.
MATHEMATICAL MASTERY
Learn how the property of reflexivity simplifies equations, proofs, and more in geometry, algebra, logic, and more.
Unlocking Reflexive Property – Key to Mathematical mastery
It may appear simple, but the implications of this property are significant. It ensures that the shapes are equal, which is a basis for proofs. Its influence goes beyond geometry. It’s an essential tool for algebra and logic. It guides us through equations, set theory, and other mathematical concepts. The reflexive property is the key to understanding mathematics in its entirety.
REFLEXIVE PROPERTY OF EVERYDAY LIFE
The reflexive property is a principle that guides us in our daily lives. The reflexive property is useful for identifying patterns, making comparisons and solving everyday problems.
Think of the symmetry in a design created by students during art class, or the balance that an athlete maintains while playing a sport. Both scenarios are examples of the reflexive property. When comparing the features or prices of different products, we use this reflexive property in order to make an informed decision.
By comparing unit prices, for example, of coffee, and examining the price per 100g we can find the most cost effective option. This property allows us to determine the true value of products, so we can make the best choices when shopping.
The reflexive property is a valuable tool that helps us navigate our daily lives with clarity and confidence.
CONCLUSUON
The reflexive property is a powerful superhero that we can trust in our everyday lives. The reflexive property has many applications, from its mathematical foundation to its practical application in real-world situations. It is an incredibly useful and strong tool that makes overcoming obstacles simple. Remember to unlock the full potential of the reflexive property as you explore the worlds of mathematics. You’ll learn to appreciate its power and how it can enrich your mathematic journey as well as your everyday life with each discovery.
Keep exploring and learning and let the reflexive properties guide you to new levels of understanding and exploration!
